Science Operations Summer Project
		HOME INDEX SEARCH HELP NEWS

Speed Limit for Altitude-Azimuth Telescopes Near the Zenith in La Silla

Karla Kauffmann

La Silla summer student, 2003

Introduction

Altitude-azimuth telescopes, as opposed to equatorial mounting, have problems when pointing at the zenith, because it requires infinite angular azimuth velocity (and acceleration) to track an object when passing through that region. There is then, a small blind spot around the zenith in which the telescope exceeds its limit speed. This zone ratio is determined by the real velocity limits of the telescope and the latitude in which it is located, in this case, La Silla.

It is important to note that, although such region exists, it means no major drawback in the celestial observation, due to the fact that this spot is very small.

Problem Description

First of all, basic definitions are needed:

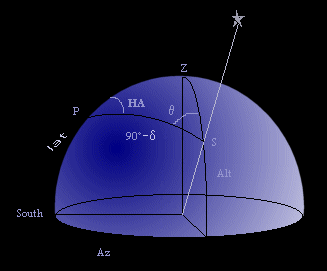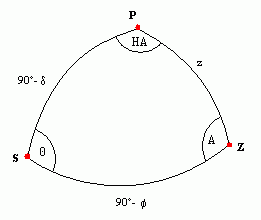Figure 1: The celestial sphere and its parameters	Figure 2: The spherical triangle that shows the relation between the different coordinate systems

The figures show the different angles, which are defined as follows:

A coordinate system transformation is necessary to adjust the equations to the data that is known. For that, spherical trigonometry is used (for further details on this matter see Wolfram research ). Listed below is a set of basic relations:

For a specified celestial source, the declination d and the latitude f are known data. If we assume that the HA has a sidereal rate of 0.25°/min (360° in 24 hours), then the rate of change of the parallactic angle is defined as:

And the rate of change of azimuth is defined as:

Both (4) and (5) in [°/min]. To simplify the notation on graphs, these quantities have been restated as dp/dH as the rate of change of parallactic angle and dA/dH as the rate of change of azimuth.

Speed Limit Analysis

With the previous definitions we are able to determine the blind spot of an Alt-Az telescope due to the restrictions on its axes speeds. These velocities are represented by dp/dH (rotator speed) and dA/dH (azimuth tracking rate).
La Silla is located at latitude: -29° 15' (29,25°) . We also know that the actual speed limits are (for azimuth and rotator) approximately 2 [°/s]. Then the real speed limit for both the azimuth and the rotator are 120 [°/min].
Using a simple program and the formulae above presented, we illustrate these speeds in function of the hour angle (time) for different declinations. To check the results we use a differential method.

The following graphs were obtained. The HA is in hours (click to enlarge):

Figure 3: Azimuth and rotator speed in [°/min] for a declination of 30°	Figure 4: Azimuth and rotator speed in [°/min] for a declination of 15°
Figure 5: Azimuth and rotator speed in [°/min] for a declination of -90°	Figure 6: Azimuth and rotator speed in [°/min] for a declination of -60°
Figure 7: Azimuth and rotator speed in [°/min] for a declination of -45°	Figure 8: Azimuth and rotator speed in [°/min] for a declination of -29°
Figure 9: Azimuth and rotator speed in [°/min] for a declination of -20°

From Figure 8, we see that, either at a declination of -29.3° or -29.2° we have values of speed that exceed the given limit ( 120[°/min] ). But for -29.1° and -29.4° (red arrows), either the azimuth or rotator speed are just below the limit. Therefore, a safe tracking is assured for any declination angle, except those in between -29.1° and -29.4° at an HA = 0 [min]. Replacing these values on equation (1), gives us an angle tracking limit on Alt-Az telescopes in La Silla. This is 89.85° or 89°51' on altitude, thus, pointing the telescopes beyond these values (e.g. the zenith: 90°), may cause them to stop or malfunction.

In practice, no Alt-Az telescopes in La Silla (NTT) are aimed past the 89° altitude.

Acknowledgments

I want to thank all the people that helped me during my summer job-studentship staying at La Silla : TIO's and astronomers on the 3p6, NTT and 2p2 telescopes, people from Engineering, Software and Site Management Department. I want to give special thanks to Olivier Hainaut for giving me this project, Ariel Sánchez for his patience, Ricardo Parra for the information on the telescope's speed limits and his humor, Paul Le Saux for helping me out on the first days, Fernando Selman and René Méndez for providing me very useful information, Gabriel Prieto and Vyerica Grbic for assisting me with this page and everyone I didn't mention here, but were vital (in some way or another) in the development of this (mini) project.

Links

• Near Zenith Tracking Limits for Altitude-Azimuth Telescopes by Borkowski, K. M.
• Pointing Model Description by Shepherd, M.
• Azimuth and Parallactic Angle Tracking near the Zenith by Ghigo, F.
• TNG Rotator Axes Motion Control by Mancini, D., Schipani, P.
• Spherical Trigonometry Relevant Relations by Gunasekera S.

References

• Watson, F. G., 1978, Mon. Not. R. astr. Soc., 183, 277-284.

Send comments to Karla Kauffmann Last update: Sep 3, 2003